Cells

I wrote a program for simulating different kinds of cellular automata in pygame.

In its most general form, a cellular automaton (CA) is defined by a number of cells, commonly arranged on a regularly tiled grid in 1, 2 or more dimensions. Each cell can be in one of a set of states (e.g. "on"/"off", "1"/"2"/"3" or "red"/"green"/"blue"). The state of a cell in the next time step is defined by its neighborhood, and can additionally depend on the current state of the cell itself. The rule that provides the next state of a cell is called a transition rule.

For example, a cell can be in one of two possible states ("on" or "off") and the state of the cell in the next time step depends on its current state and also the states of its 8 neighbors. Then, the number of possible transition rules is equal to the number of possible states (2) raised to the number of cells in its "neighborhood" (8 neighbors + itself): 2 ** 9 = 512.

Here is a 2D CA with 2 states (black and white) and a "Moore" neighborhood with randomly generated transition rules:

Here is one with 3 states (black, white and red):

And here is one with 3 states and a "von Neumann" neighborhood of radius 2:

The best known cellular automaton is Conway's "Game of Life Here, the transition rule does not depend on the absolute configuration of neighbors but on the sum of their states (totalistic CA). The "Game of Life" usually uses 2 states ("off" and "on") and a "Moore" Neighborhood.

An "off" cell with exactly 3 "on" neighbors is "born" ("off" -> "on") and a cell with exactly 2 or 3 neighbors "survives" "on" -> "on"). A cell with 0, 1, 4, 5, 6, 7 or 8 "on" neighbors "dies" ("on" -> "off").

Also, rules can be probabilistic rather than deterministic. Such cellular automata are called probabilistic cellular automata. A probabilistic rule gives, for each neighborhood, the probabilities that the central cell will transition to a different state in the next time step.

For example using the transition rules for "Game of Life", but on each time step there is a 0.1% probability that each cell will transition to the opposite state:

All rules for "Life-like" cellular automata can be expressed in B/S notation. Where "B" stands for the conditions at which "dead" cells are "born" (off -> on) and "S" stands for the conditions at which "alive" cells "survive" (on -> on). All "alive" cells that do not meet any of the "survival" conditions "die" (on -> off). For example "Conway's Game of Life" has the rulestring B3/S23. There are 262144 (= 2^18) possible rules for "Life-like" cellular automata.

Here is an example of a Life-like cellular automaton with the rulestring "B35678/S4678" ("Holstein"):

Each cell can follow a different rule. In the following example new cells are born, when one or more neighboring "parent" cells contain the total number of neighbors in their "B" rule. The rulestring of the new cell is chosen randomly from one of its "parents". Each rule is rendered in a distinct color.

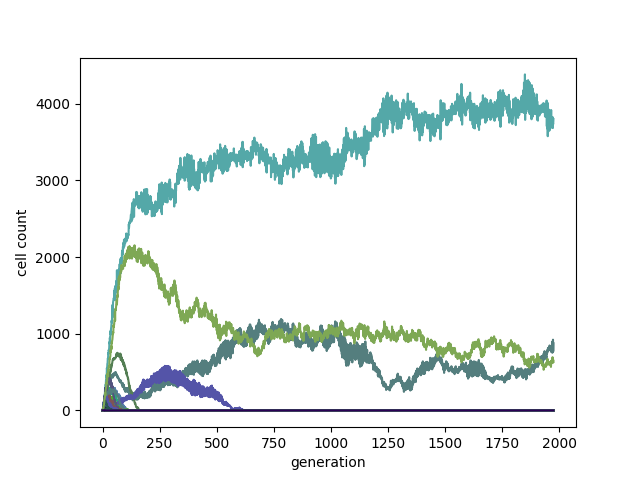
The top surviving cells have the rules:
B1234567/S023: 71.6%
B1234578/S0: 16.51%
B1345678/S23: 11.89%

The above rule can be combined with a genetic algorithm that introduces random mutations:

Cellular automata can also be used to simulate logical circuitry in which each cell uses a distinct transition rule.

This rule discribes a function that computes the current state of the cell from the states of the surrounding cells. In a two dimensional grid, where all cells are aligned horizontally and vertically, each cell is surrounded by 8 other cells (also called the Moore neighborhood).

If each cell gives 1 bit of information to each of its neighbors, we can say that each cell has an output (o) of 8 bits and also an input (i) of 8 bits (or 1 byte) at any given point of time.

We can now define a function that outputs an 8 bit value for every 8 bit input:

f((i₀, i₁, i₂, i₃, i₄, i₅, i₆, i₇)) = (o₀, o₁, o₂, o₃, o₄, o₅, o₆, o₇)

One way of defining such a function would be by using a lookup table for all possible inputs (with 256 entries).

00000000	00000100
00000001	00101000
00000010	00001100
00000011	01000000
...	...
11111111	00001000

Of course, this function can also be defined in any other suitable way, as long as it outputs one byte of information for every byte of input. For example, the following function describes a cell, that relays just one bit of information from its westward side to the opposite side:

func(i0, i1, i2, i3, i4, i5, i6, i7):
    o2 = i6
    return(0, 0, o2, 0, 0, 0, 0, 0)

A slightly more complex example would be a cell that only performs this action when a second input is present (a switch):

func(i0, i1, i2, i3, i4, i5, i6, i7):
    o2 = i6    
    if i0 == 1:
        return(0, 0, o2, 0, 0, 0, 0, 0)
    else:
        return(0, 0, 0, 0, 0, 0, 0, 0)

As can be easily demonstrated, this way every cell is capable of any logical operation and the automaton has the capability of universal computation. For example a single cell is capable of 4 bit addition:

s₄s₃s₂s₁s₀ = a₃a₂a₁a₀ + b₃b₂b₁b₀

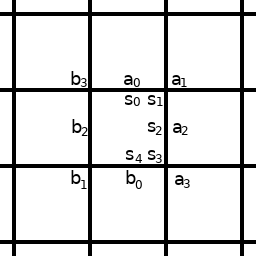
func(i0, i1, i2, i3, i4, i5, i6, i7):
    a = (i0, i1, i2, i3)
    b = (i4, i5, i6, i7)
    
    sum = []

    carry = 0

    for i in range(4):
        s = a[i] + b[i] + carry
        if s > 1:
            carry = 1
        else:
            carry = 0
        s = s % 2
        sum.append(s)

    sum.append(carry)

    return(sum[0], sum[1], sum[2], sum[3], sum[4], 0, 0, 0)

All in all there are 256^256 possible ways to map 265 bytes of input to 265 bytes of output. From which follows that there are just as many possible rules for each cell.

Cellular automata can also be used to simulate biochemical processes by defining rules that emulate movement and interaction of biomolecules.

The following example simulates a living cell (white) with DNA (red) that codes for vesicles (gray) that merge with the cell membrane and make it grow. The translation DNA into vesicles is performed by a ribosome (black).